Дискретное интегрирование

Иногда показания различных датчиков подлежат интеграции. Чаще всего это происходит с гироскопами (гиротахометрами, если быть верным), применяемыми для стабилизации таких устройств, как квадрокоптеры. В этой статье разберём дискретное интегрирование и поговорим о методах его реализации на основе цифровых устройств.

Метод прямоугольников

Вспомним, что определённый интеграл равен площади, заключённой между графиком подынтегральной функции и осью абсцисс.

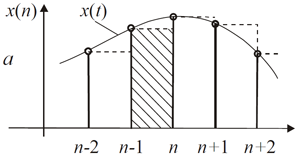
Самым простым методом его вычисления является метод прямоугольников: площадь искомой фигуры делится на равные по ширине (по длительности промежутка измерения) прямоугольники (как на рисунке выше), площадь всех прямоугольников складывается.

Все площади складываем последовательно, то есть на шаге nнужно будет произвести такое действие:

где:
y(n) — текущая величина интеграла;
y(n-1) — величина интеграла на прошлом шаге;
x(n-1) — величина подынтегральной функции на прошлом шаге;
Т — добавленное на этом шаге время.

Говоря проще, мы поочерёдно измеряем площади всех прямоугольников (на рисунке закрашен пунктиром) и складываем их с уже имеющейся.

Метод трапеций

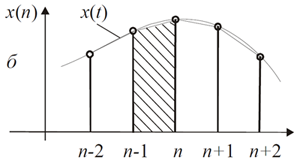
Так как предыдущий метод может быть недостаточно точным, можно применить этот. Суть остаётся всё той же, единственное отличие – вместо прямоугольников используются трапеции и их площадь вычисляется несколько иначе.

Как можно заметить на рисунке, трапеции позволяют гораздо более точно оценить площадь между осью абсцисс и графиком подынтегральной функции.

Площадь трапеции равна двум её сторонам помноженным на высоту и делённым пополам.

Благодаря этому уравнение для этого метода станет таким:

Использование данного метода всё также не исключает заметные погрешности. Для их устранения используются методы, более точные и сложные, но при этом слишком ресурсоёмкие для микроконтроллеров.

Физический смысл интеграла

Разберём движение равноускоренного (или равнозамедленного) тела. Обозначим ускорение буквой a. Функция зависимости ускорения от времени станет такой:

Интегрируем её для получения функции зависимости скорости (v) от времени (t):

Следующим интегрированием получаем зависимость пройденного расстояния (s) от времени:

Итак, сделаем вывод. При известной скорости тела можно без особого труда найти пройденное им за определённое время расстояние.

Интегрирование показаний гироскопа

Переходим непосредственно к практическому применению дискретного интегрирования. Мы будем получать показания с гироскопа. На самом деле, обычные гироскопы определяют совсем не угол отклонения от своей оси, а скорость его же углового вращения. То есть, он является не гироскопом, а гиротахометром.

Теперь вспомним предыдущую главу: при известной скорости тела, можно найти пройденное им расстояние, в случае с гиротахометром – угол наклона.

Угол angleвыражен градусами Эйлера, скорость aspeed – ими же в секунду. Будем вычислять интеграл прямоугольниками. То есть через равные промежутки времени длительностью delta начнём измерять площадь текущего прямоугольника и складывать её к ранее вычисленной площади:

Скетч для Arduino и гироскопа Pololu LPR550AL. Каждые 100 миллисекунд он отправляет в COM-порт угол поворота гироскопа.

const int gyrPin = A0;
const int INTEGR_DELAY = 20;
const int SERIAL_DELAY = 100;
 
// Датчик Pololu LPR550AL
const float vref = 3.3;
const float vzero = 1.23;
const float sens = 0.0005;
const float adc = 1023;
 
int integr_time, serial_time, real_delta;
short gyr_raw;
float angle, aspeed;
 
void setup() {
    Serial.begin(9600);
    angle = 0;
}
 
void loop() {
    // Интегрирование скорости поворота гироскопа
    time = millis();
    real_delta = time - integr_time;
    if( real_delta > INTEGR_DELAY ){
        integr_time = time;
        gyr_raw = analogRead(gyrPin);
        aspeed = ((gyr_raw * vref)/adc - vzero)/sens;
        angle = angle + aspeed * real_delta;
    }
 
    // Отправка угла через последовательный порт на ПК
    time = millis();
    if( time - serial_time > SERIAL_DELAY ){
        serial_time = time;
        Serial.print(angle, 4);
    }
}

const int gyrPin = A0;

const int INTEGR_DELAY = 20;

const int SERIAL_DELAY = 100;

// Датчик Pololu LPR550AL

const float vref = 3.3;

const float vzero = 1.23;

const float sens = 0.0005;

const float adc = 1023;

int integr_time, serial_time, real_delta;

short gyr_raw;

float angle, aspeed;

void setup() {

Serial.begin(9600);

angle = 0;

}

void loop() {

// Интегрирование скорости поворота гироскопа

time = millis();

real_delta = time - integr_time;

if( real_delta > INTEGR_DELAY ){

integr_time = time;

gyr_raw = analogRead(gyrPin);

aspeed = ((gyr_raw * vref)/adc - vzero)/sens;

angle = angle + aspeed * real_delta;

}

// Отправка угла через последовательный порт на ПК

time = millis();

if( time - serial_time > SERIAL_DELAY ){

serial_time = time;

Serial.print(angle, 4);

}

Датчик является аналоговым. Для конвертирования значения напряжения на его выходе использовалось выражение:

Значения vref, vzeroи sens (опорное и нулевое напряжения, чувствительность) нужно брать указанные в даташите на применяемый гироскоп.

Повышение точки интегрирования

Точность вычисления интеграла возрастает обратно пропорционально длительности отрезка дискретизации. В скетче выше она составляет 20 миллисекунд, этого вполне хватает для стабилизации беспилотников. Если позволяет мощность микроконтроллера – для повышения точности можно уменьшить этот отрезок.

Также можно изменить принцип интегрирования, воспользовавшись методом трапеций, как вариант. Сложность программы не сильно возрастёт:

const int gyrPin = A0;
const int INTEGR_DELAY = 20;
const int SERIAL_DELAY = 100;
 
// Датчик Pololu LPR550AL
const float vref = 3.3;
const float vzero = 1.23;
const float sens = 0.0005;
const float adc = 1023;
 
int integr_time, serial_time, real_delta;
short gyr_raw;
float angle, old_aspeed, aspeed;
 
void setup() {
    Serial.begin(9600);
    angle = 0;
    aspeed = 0;
}
 
void loop() {
    // Интегрирование скорости поворота гироскопа
    time = millis();
    real_delta = time - integr_time;
    if( real_delta > INTEGR_DELAY ){
        integr_time = time;
        gyr_raw = analogRead(gyrPin);
        aspeed = ((gyr_raw * vref)/adc - vzero)/sens;
        angle = angle + (aspeed + old_aspeed) * real_delta / 2;
        old_aspeed = aspeed;
    }
 
    // Отправка угла через последовательный порт на ПК
    time = millis();
    if( time - serial_time > SERIAL_DELAY ){
        serial_time = time;
        Serial.print(angle, 4);
    }
}

const int gyrPin = A0;

const int INTEGR_DELAY = 20;

const int SERIAL_DELAY = 100;

// Датчик Pololu LPR550AL

const float vref = 3.3;

const float vzero = 1.23;

const float sens = 0.0005;

const float adc = 1023;

int integr_time, serial_time, real_delta;

short gyr_raw;

float angle, old_aspeed, aspeed;

void setup() {

Serial.begin(9600);

angle = 0;

aspeed = 0;

}

void loop() {

// Интегрирование скорости поворота гироскопа

time = millis();

real_delta = time - integr_time;

if( real_delta > INTEGR_DELAY ){

integr_time = time;

gyr_raw = analogRead(gyrPin);

aspeed = ((gyr_raw * vref)/adc - vzero)/sens;

angle = angle + (aspeed + old_aspeed) * real_delta / 2;

old_aspeed = aspeed;

}

// Отправка угла через последовательный порт на ПК

time = millis();

if( time - serial_time > SERIAL_DELAY ){

serial_time = time;

Serial.print(angle, 4);

}

Подведем итоги

Теперь мы умеем интегрировать угловую скорость гиротахометра и вычислять угол его поворота. Эти знания позволят воплотить в жизнь простую систему стабилизации для беспилотных аппаратов, в частности, распространённых квадрокоптеров.

Для стабилизации полёта этого будет достаточно, но автоматическое управление полётом вряд ли получится реализовать из-за дрейфа нуля у гиротахометра. Справиться с ним поможет комплементарный фильтр, использующий показания акселерометра и гиротахометра. Но это уже следующий уровень и тема для другой статьи.

Дискретное интегрирование

Метод прямоугольников

Метод трапеций

Физический смысл интеграла

Интегрирование показаний гироскопа

Повышение точки интегрирования

Подведем итоги

Смотрите также